自然对数和数学常数e是数学中非常重要的概念,涉及到微积分、复变函数、概率论、物理等多个领域。本文将详细介绍自然对数和数学常数e的定义、性质和应用,帮助读者深入理解这两个数学概念,并体会其在实际问题中的运用。
自然对数是以e为底的对数函数,用符号ln(x)表示。其中x是一个正实数(x0),而e是一个数学常数,约等于2.718281828459。
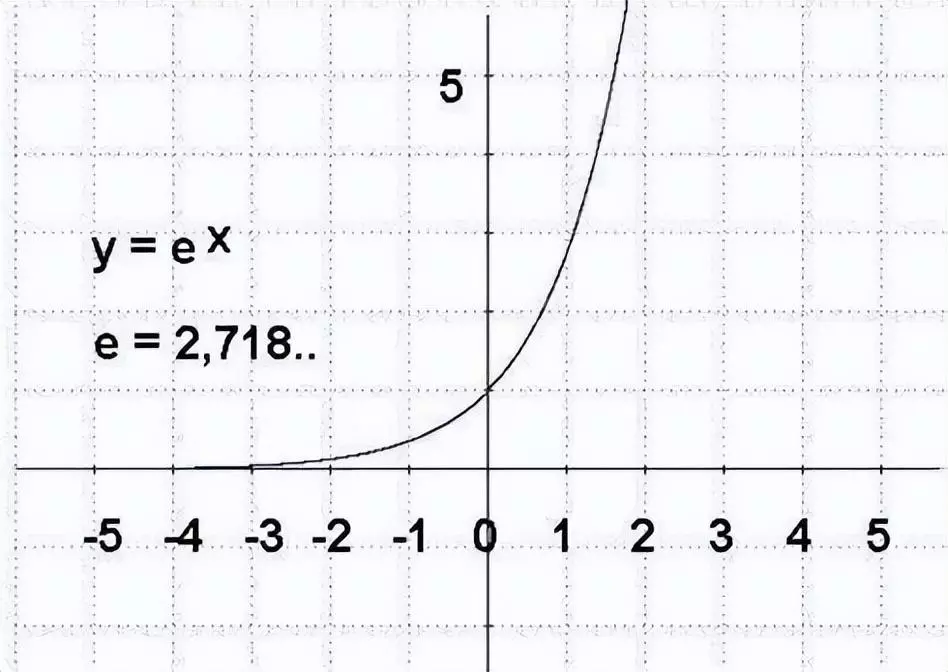
自然对数的图像是一条光滑的曲线,在x轴上方,且当x=1时,y=0。自然对数的定义可以表示为:
ln = ∫ dt/t
其中,∫表示积分,t是自变量,dt/t表示函数的导数。这个式子表明,自然对数是一个积分函数,它的导数是1/x。因此,自然对数可以看做是一个反函数,把以e为底的指数函数e^x变成了一个由x映射到y=ln(x)的函数。
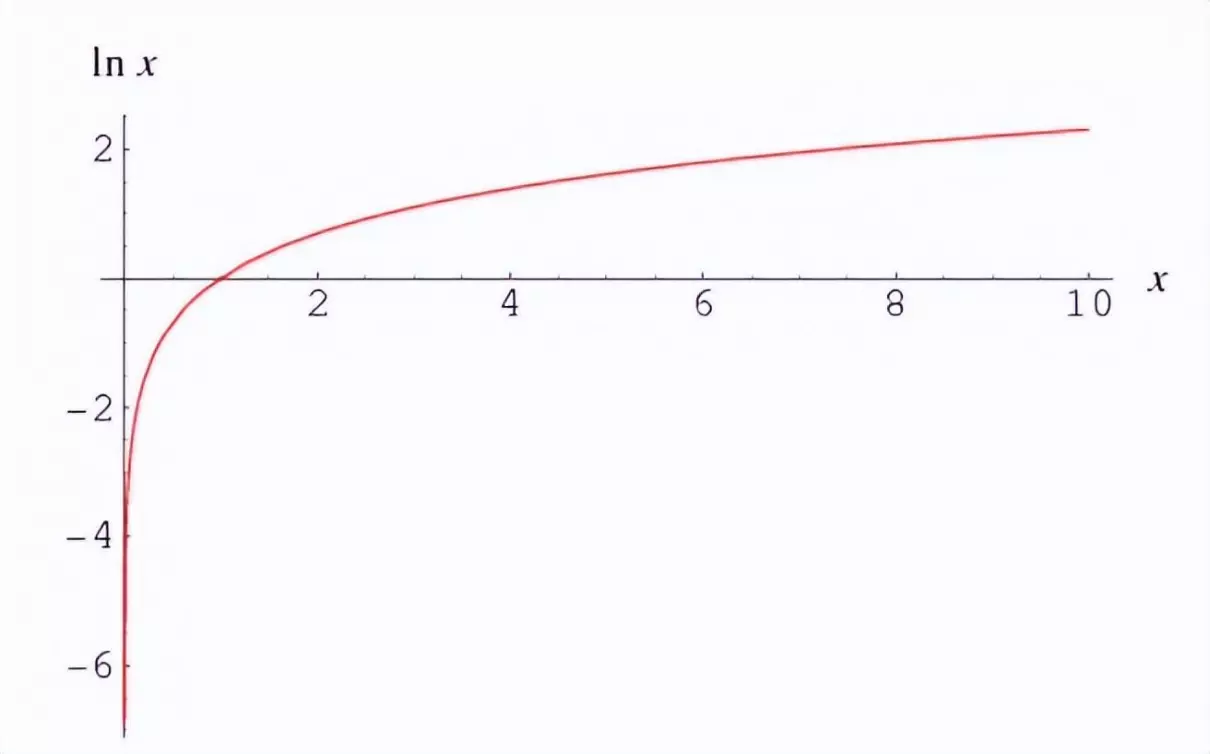
由此,我们可以考虑一个实际问题:在化学反应中,溶液中某种反应物的浓度随时间的变化规律可以用一个指数函数表示。
假设在初始时刻t=0时,该反应物的浓度为C0。现在我们想知道,在任意时刻t,该反应物的浓度与初始时刻的浓度相比变化了多少倍。这个问题可以通过自然对数来回答,即设该反应物的浓度随时间t的变化规律为C = C0*e^,其中k是一个正常数。则在任意时刻t,该反应物的浓度与初始时刻的浓度相比变化了多少倍,可以用自然对数来表示,即
ln = ln) = -kt
这个式子表明,该反应物的浓度随时间的变化率是一个负的常数k,而在任意时刻t,其浓度与初始时刻的浓度相比变化了e的-k*t次方倍。
数学常数e是自然对数的底数,它的值约为2.718281828459。e的定义可以从复利计算中得出。假设有一个本金为1元,年利率为100%的银行账户,如果每年复利一次,那么在第n年的末尾,账户余额将会是1*(1+1/n)^n元。当n趋近于无穷大时,这个式子的极限值就等于e。因此,数学常数e可以表示为:
e = lim ^n
这个式子表明,数学常数e是一个极限值,它可以用无穷级数来表示。具体来说,e可以表示为:
e = 1/0! + 1/1! + 1/2! + 1/3! + ...
其中,0!表示0的阶乘,n!=1*2*3*...*n表示n的阶乘。这个无穷级数是发散的,但是前面的几项可以作为e的一个很好的近似值。
我们可以考虑一个实际问题:在统计学中,当样本容量非常大时,样本均值的分布会趋近于正态分布。而正态分布的密度函数又涉及到数学常数e的指数函数。
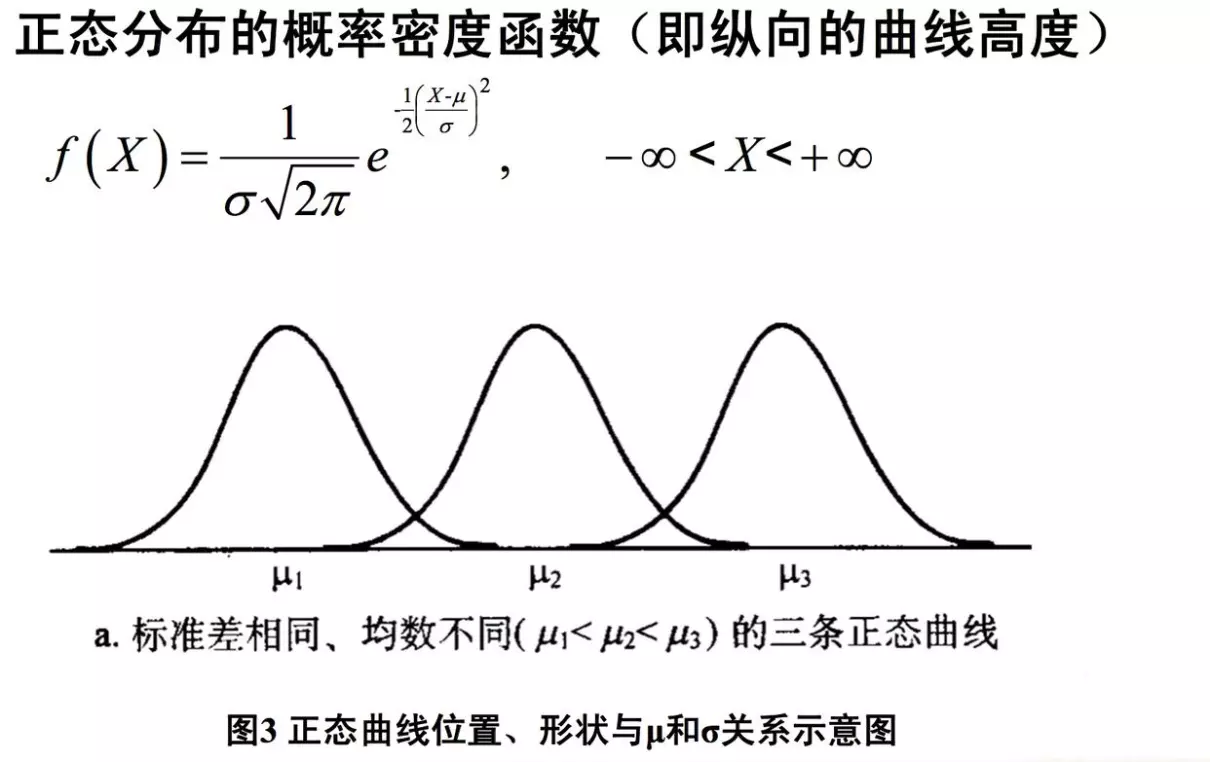
假设我们有一个样本容量为n的随机样本,其样本均值为X̄,样本标准差为S。如果我们对样本均值进行标准化处理,即令Z=(X̄-μ)/(S/√n),其中μ是总体均值,则Z的分布会趋近于标准正态分布N(0,1)。这个标准正态分布的概率密度函数为:
f = ) * e^
其中√表示开方,π表示圆周率,e表示数学常数e。这个式子表明,标准正态分布的密度函数是一个关于z=0对称的钟形曲线,在z趋近于正无穷或负无穷时,密度趋近于0,在z=0时取得峰值。这个密度函数中涉及到了数学常数e的指数函数。
自然对数和数学常数e具有一些非常重要的性质,如下所示:
3.1、自然对数在定义域内是单调递增的,即ln ln 当且仅当x1x2.
这个性质表明,自然对数可以用来比较不同实数的大小关系,并且在这个过程中保持大小关系不变。
自然对数的导数是1/x,即d/dx ln = 1/x
这个性质表明,自然对数是一个可微函数,并且其导函数可以用自然对数本身来表示。数学常数e是一个超越数,也就是说,它不是任何有理数(如整数、分数)的根。这个性质表明,数学常数e是一个非常特殊的数,它与其他任何有理数都存在本质区别。
3.2、自然对数和指数函数e^x是彼此的反函数,即ln = x 和 e^) = x
这个性质表明,自然对数和指数函数是一对互逆的函数,它们可以相互转化和应用。
自然对数和数学常数e在数学和物理中有着广泛的应用。例如:
4.1微积分中的微分和积分都可以用自然对数和指数函数表示。
例如,考虑一个函数f = ln。我们可以用微积分的方法求出f的导函数为f' = 1/-2x/。一般情况下,f的导函数无法用有限次的简单函数表示,但是如果我们将f表示为f = ln = ln-ln,则f的导函数可以分别用自然对数和指数函数表示为:
f' = d/dx - d/dx
= 1/x - 2x/(x^2+1)/(x^2+1)
= (x^2-1)/(x(x^2+1))^2
复变函数中的欧拉公式e^ = cos + isin就涉及到了数学常数e和三角函数的关系。
欧拉公式是数学中非常重要的公式之一,它将指数函数、三角函数和虚数单位i联系在了一起。这个公式可以用泰勒级数的方法推导出来,即:
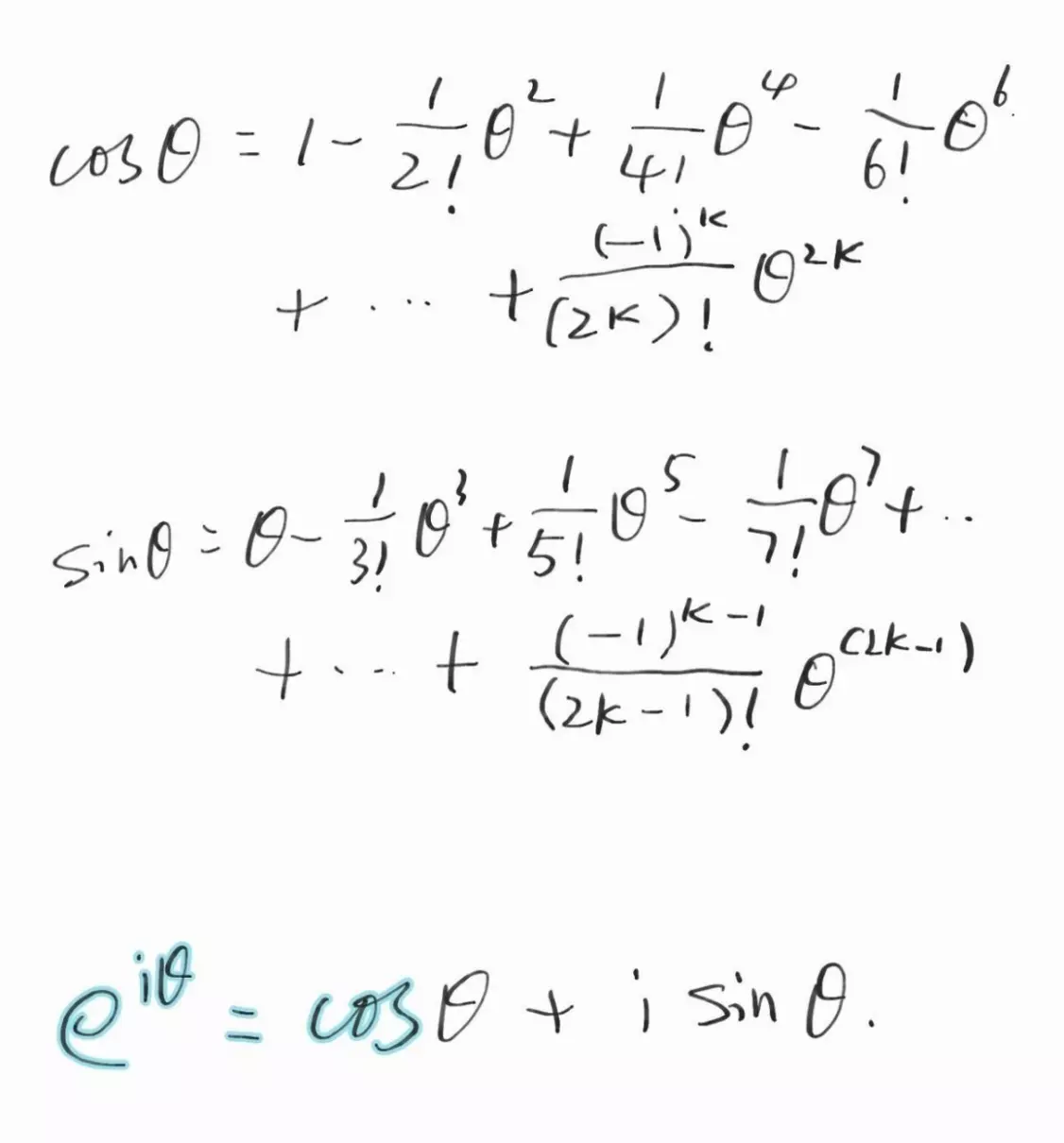
这个式子表明,三角函数和指数函数之间存在本质联系,而数学常数e是这种联系的一个重要因素。
4.2 概率论中的指数分布函数和泊松分布函数都涉及到了自然对数和指数函数。
在概率论中,指数分布函数和泊松分布函数是非常重要的分布函数。其中,指数分布函数表示等待时间在一个确定的时间内发生事件的概率分布,而泊松分布函数表示在一个单位时间内事件的发生次数的概率分布。这两个分布函数都可以用自然对数和指数函数来表示。
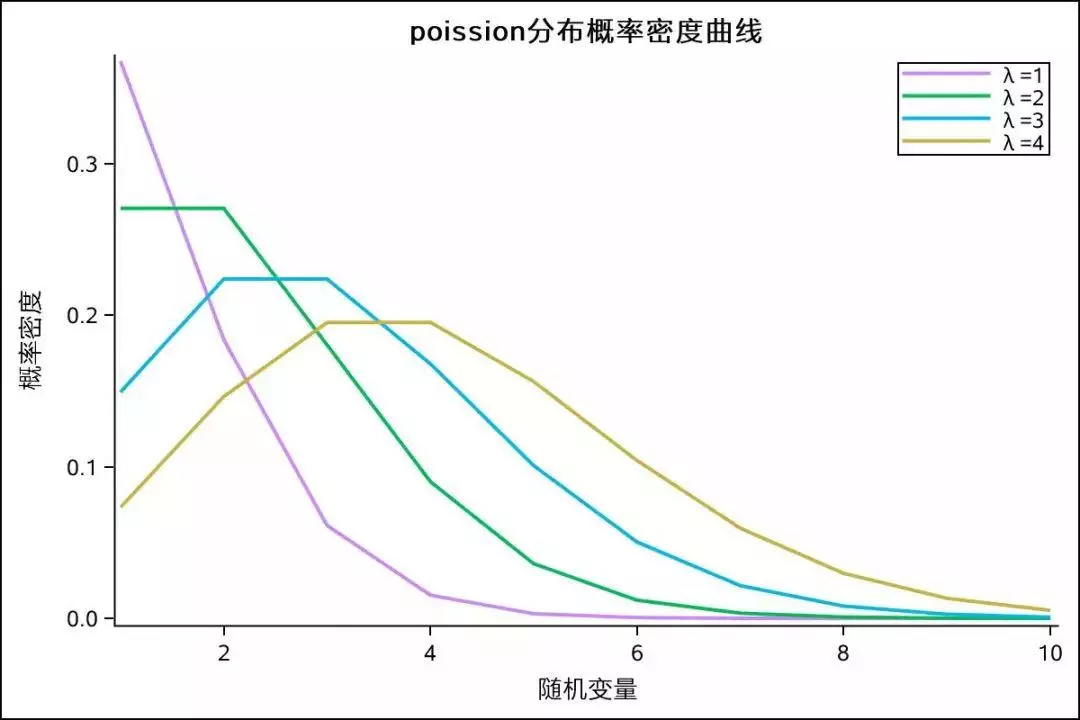
泊松分布
举例来说,考虑指数分布函数,其概率密度函数为:
f = λe^
其中λ是一个正常数。这个概率密度函数可以通过自然对数和指数函数来表示:
f = λe^ = λe^
= λe^(-λx)*e^(ln(λ))
4.3 物理中的放射性衰变、振荡电路等现象都可以用自然对数和指数函数来描述。
在物理中,放射性衰变、振荡电路等现象都涉及到了自然对数和指数函数。
举例来说,考虑一个放射性样品,其衰变速率随时间的变化规律可以用指数函数表示。假设该样品初始时刻的放射性核数为N0,其衰变速率为λ,则在任意时刻t,其放射性核数N(t)与初始时刻的核数N0的比值可以用自然对数和指数函数表示:
N/N0 = e^
这个式子表明,在任意时刻t,放射性核数与初始时刻的核数N0的比值是一个以指数函数衰减的形式变化的。
自然对数和数学常数e是数学中至关重要的概念,它们不仅具有理论上的意义,而且具有广泛的实际应用。通过了解自然对数和数学常数e的定义、性质和应用,可以扩展我们的数学知识,提高数学应用能力,进一步认识数学在各行各业中的重要作用。