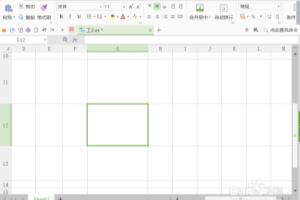
如图所示,函数fx的图像由指数函数fx等于b的x密于密函数gx等于x的a次方拼接而成。其中,m等于a的a次方,n等于a的b次方,p等于b的a次方,q等于b的b次方。用小于号连接mn、pq的大小关系。
在看到这个问题时,首先要看图像。图像的突破口是当x等于1/4时,y等于1/2。让我们一起来连接这个突破口。因为指数函数xfx等于b的x方,只需要将其写成x等于1/4时,密函数等于1/2时,都等于1/2,代入be的x方,be的1/4就等于1/4的a次方,b等于1/16。

接下来,让我们看看mn、pq分别等于多少。m就等于a的a次方,等于都写成1/2的1/2次方,n等于a的b次方,它就等于1/2的1/16,ab代入就行,p等于b的a次方,它等于1/16的1/2。
为了更好地比较,将其转化为数字。这个是1/2,将其转化为1/4次方,4乘以1/2这一个是2。再来看一下k,它等于b的b次方,等于1/16的1/16,同样将其转化为1/2的1/4次方。

现在,我们已经画出了mn、pq的图像。让我们比较一下它们。这两个函数都等于类似的函数,y等于1/2的x方。这是一个减函数,因此我们无需考虑1/2。先看指数2是最大的,小于1/2的1/2,再看小于1/2的1/4,再看小于最后的1/2的1/16。这是一个减函数,指数越大,数越小。因此,p小于m,小于q小于n,直接写上即可。最后,写上是p小于m,小于q小于n。
这一期完成。