在数学上有一种很重要的思想,“抓基础、重转化”是学好数学、解决数学问题的一个重要手段。所谓“转化思想”就是通过一定的数学手段把未知问题转化为已知问题,把复杂问题转化为简单问题,把隐性问题转化为显性问题,从而使未知陌生的问题变得更为熟悉,复杂问题更为简单,隐藏条件变得更为显露,达到解决问题的目的。
在数学上我们经常使用的两个转化手段,辅助图形和辅助参数,下面我们分别举例说明。
一、辅助图形
在一些复杂的几何问题或函数问题中,根据题目的需要作一些几何图形如线段、曲线、几何图形等辅助图形,拓宽题目的条件,达到化未知为已知,化隐为显之目的,从而使问题解决。
(一)构造辅助线段
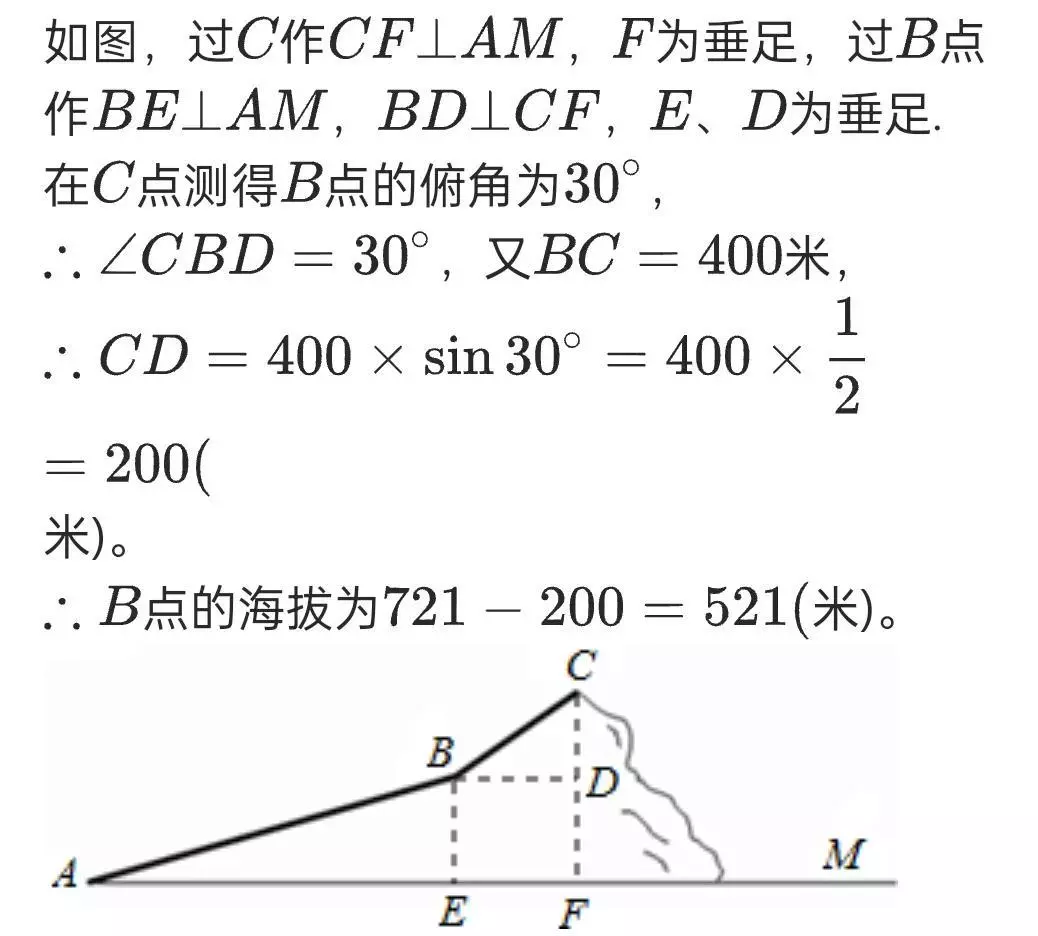
【反思】根据题目的条件通过作垂线段构造直角三角形,把题目中孤立的条件相互联系,通过解直角三角形来解决。像这种作辅助线的特点通过作辅助线段补全包含某些残缺的定理图形,便于利用定理知识解决问题,这就要求同学们学习定理时要从定理的文字语言、图形语言、符号语言三个方面了解掌握,而不能只记定理的文字叙述,另外要增强识图能力,要从复杂的图形背景中发现包含定理的图形或残缺的定理图形。
(二)构造辅助曲线
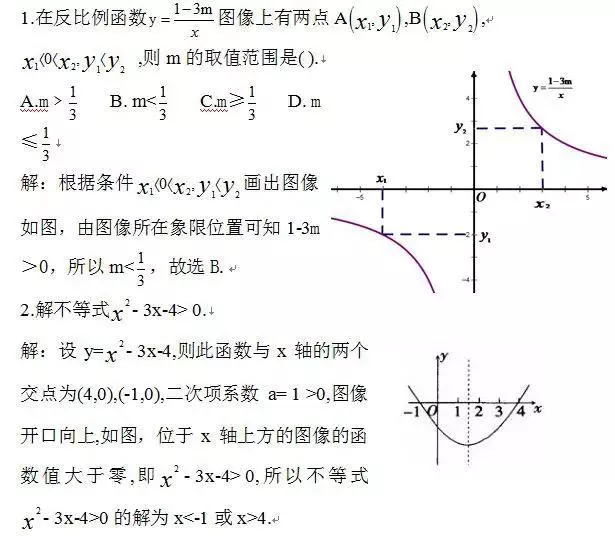
【反思】在解决函数的问题时,有些时候利用数形结合巧妙构造函数图象转化为函数图象问题时,使抽象问题更为直观。
(三)构造辅助图形
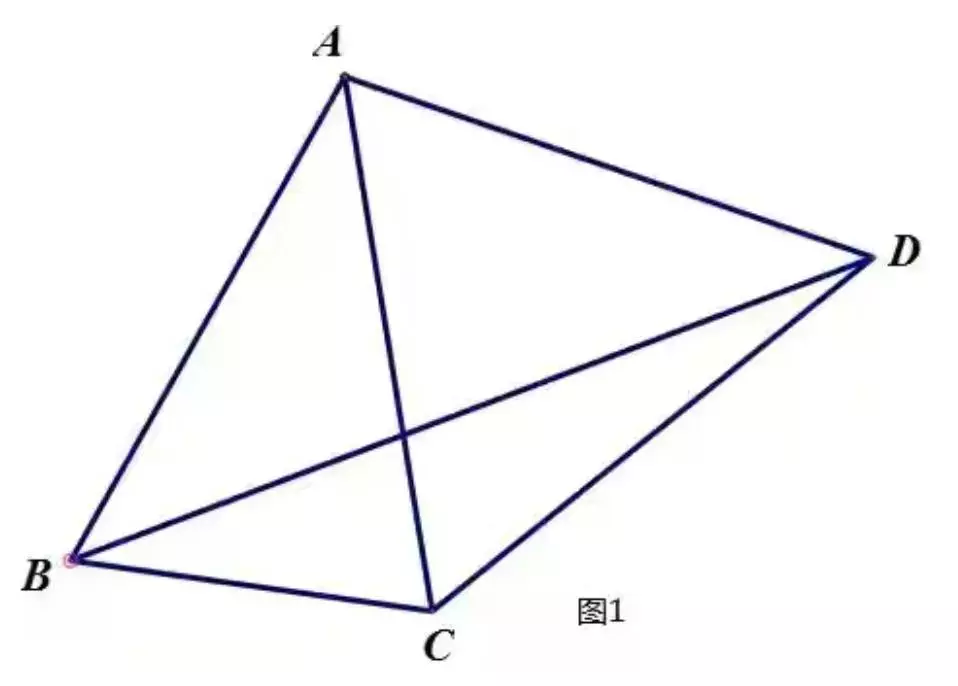
解:∵AB=AC=AD
∴根据圆的定义特征点B、C、D在以点A为圆心,AB为半径的圆上(如图5)
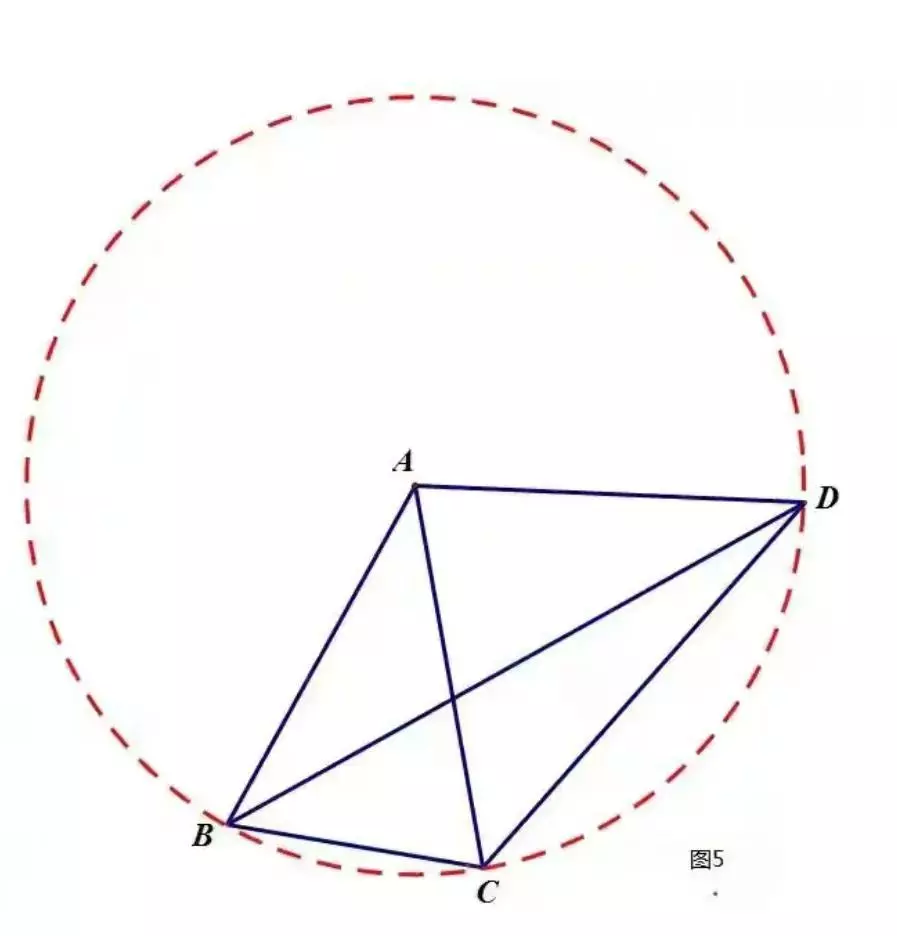
∴根据同圆上一段弧所对的圆周角等于这段弧所对圆心角度数的一半可得∠BDC=½∠BAC=½×40⁰=20⁰.
【反思】作辅助圆的前提是了解圆上点的特征,解几何题不要认为作辅助线只是连接线段,甚至可以作辅助图形,如本题中的辅助圆。
二、辅助参数
在解决代数中的某些数量问题时,为构造代数式、方程、方程组、不等式、不等式组、函数关系式等,需要设某些参量字母,来构造数式、等式,利用代数知识解决问题。
(一)设参量字母解决数式问题
比较2021×20232023
与2023×20212020的大小关系.
解:设2023=t。
则2021×20232023
=(t-2)(10000t+t)
2023×20212020
=x[10000(t-2)+(t-3)]
∴2021×20232023
-2023×20212020
=(t-2)(10000t+t)-t[10000(t-2)+(t-3)]
=10000t(t-2)+t(t-2)-10000t(t-2)-t(t-3)
=t(t-2)-t(t-3)
=t=20230
即2021×202320232023×20212020
【反思】设而不求
仔细观察题目中的数字,可以发现其实是由三个数“2020、2021、2023”有规律地排列的,特别地。
20 232 023=20 230 000+2023。
20 212 020=20 210 000+ 2020。
我们只需选其中一个用字母表示,其余…的可以用含此字母的代数式表示,这样就可以将“数”乘转化为“式”乘,再应用作差法比较所得新的代数式的大小.直接计算也可以比较这两个数的大小关系,但计算量较大且过程复杂、繁琐,容易出错.
(二)设未知参量列方程(组)或函数关系式解决实际问题
某商店购进一批单价为18元的商品, 如果以单价20元出售,那么- -个星期可售出100件.根据销售经验,提高销售单价会导致销售量减少即当销售单价每提高1元,销售量相应减少10件,如何提高销售单价,才能在一-个星期内获得最大利润?最大利润是多少?
解:设售价提高x元,总利润为W元,由题意。
得W = 。
W=-10(x一4)²十360.
∵a=-10 0。
当x=4时,W最大=360元.
答:售价提高4元时,才能在一-个星期内获得最大利润,最大利润是360元.
【反思】设未知数列方程或列函数关系式解应用题实际也是一种设参法。
(三)设参换元解方程组

【反思】换元法,即解题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化的方法.换元法又称辅助元素法、变量代换法.换元法是一种重要的解题方法.通过引进新的变量,可以把分散的条件联系起来,隐含的条件显露出来,或者把条件与结论联系起来.或者变为熟悉的形式,把复杂的计算和推证简化.
(四)设参解决有关比例的问题

【反思】有些参量只是参与过程,不影响最后的结果,起到化难为易,化抽象为具体,化繁为简,起一个牵线搭桥的作用。
(五)设参量解决几何图形问题
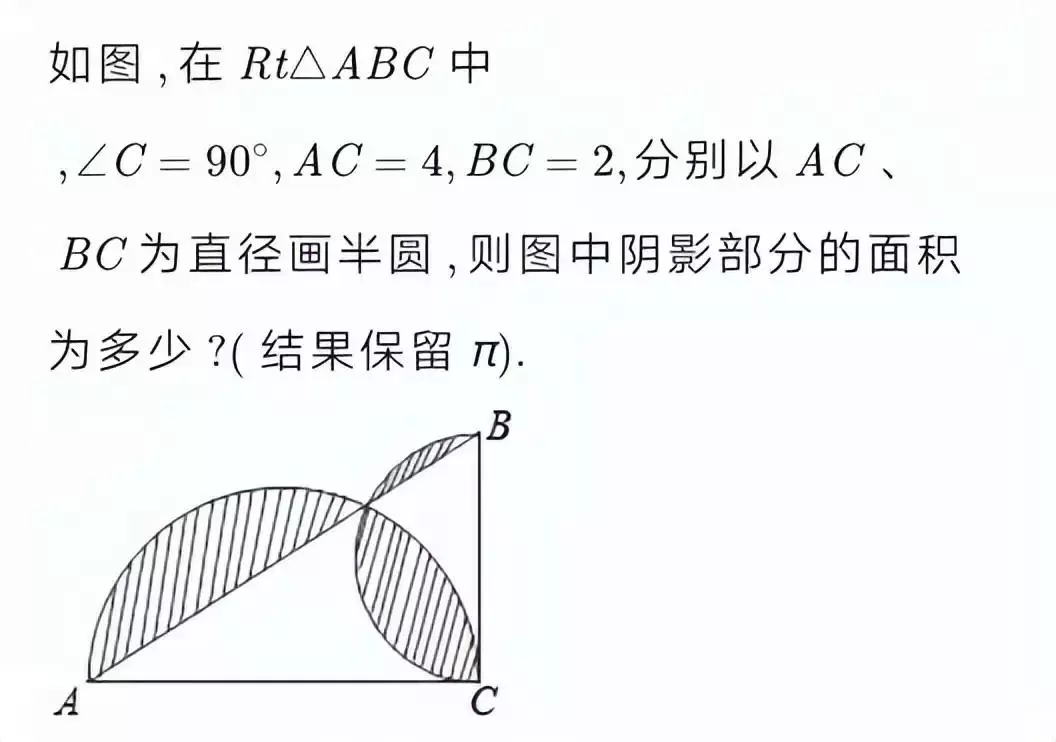
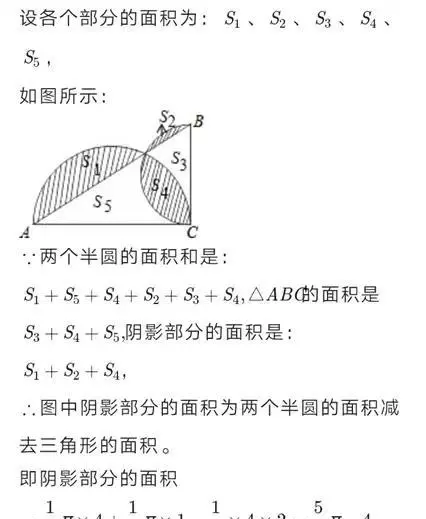
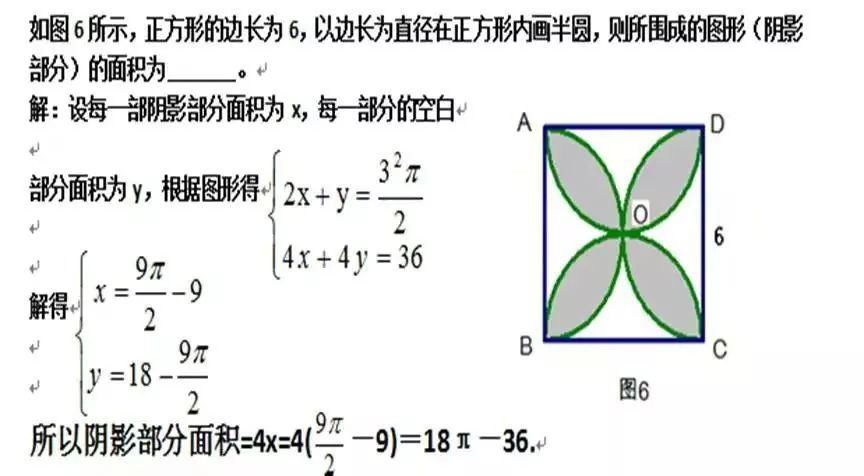
【反思】几何图形部分重叠覆盖形成阴影叠图,设参数或未知数构造代数式或方程方程组方法求阴影的面积。
三、用辅助手段进行公式、定理的证明
作辅助图形证明勾股定理(“形”证“形”)
如图6
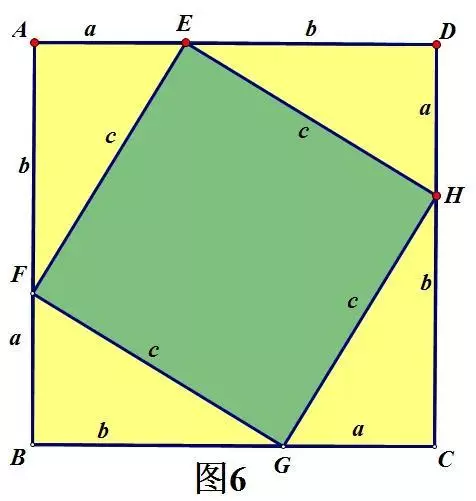
S正方形ABCD-S正方形EFGH=4S.
所以:(a+b)²-c²=4×½ab
即a²+2ab+b²-c²=2ab
从而,可得a²+b²=c².
证法二
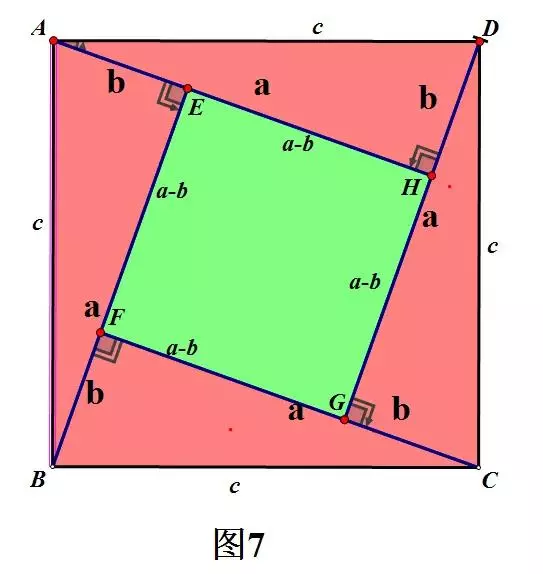
S正方形ABCD-S正方形EFGH=4S.
所以:c²-(a-b)²=4×½ab
即c²-(a²-2ab+b²)=2ab
从而,可得a²+b²=c².
证法三——总统证法
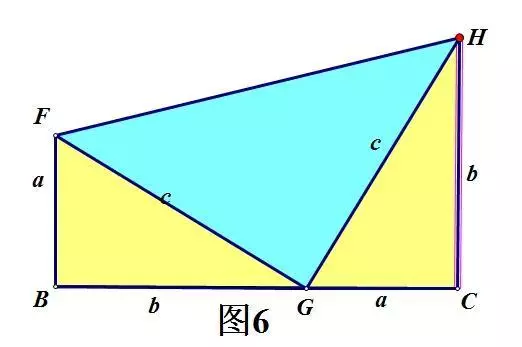
S梯形BCDHF
=SΔBFG+S+S.
所以:
½(a+b)(a+b)
=½c²+½ab+½ab
即a²+2ab+b²=c²+ab+ab
从而,可得a²+b²=c².
(二)作辅助图形证完全平方公式(“形”证“数”)
(a-b)²=a²-2ab+b²
如图5。
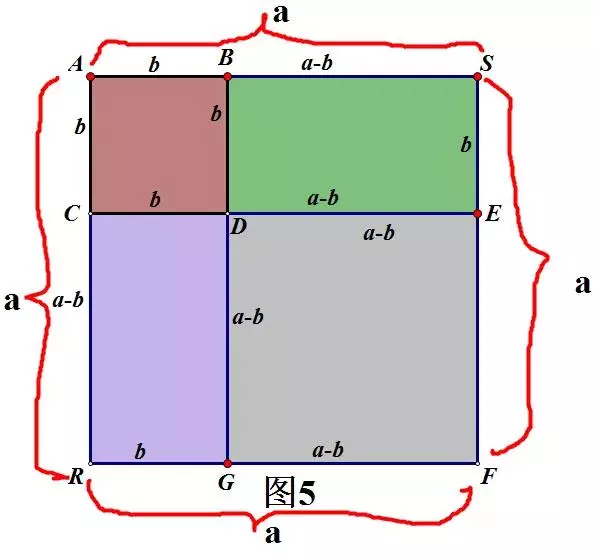
由S正方形DGFE=S正方形ARFS-S矩形ACES-S矩形ARGB+S正方形ABDC
即(a-b)²=a²-ab-ab+b²
整理可得:(a+b)²=a²-2ab+b²
(a+b)²=a²+2ab+b²
如图4。
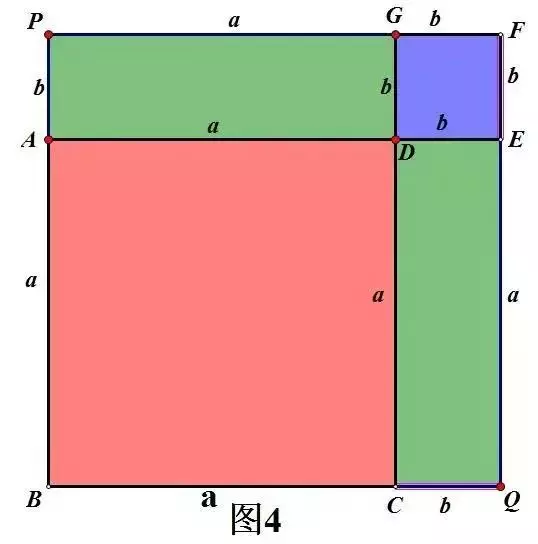
由S正方形PBQF=S正方形ABCD+S矩形PADG+S矩形CDEQ+S正方形GDEF