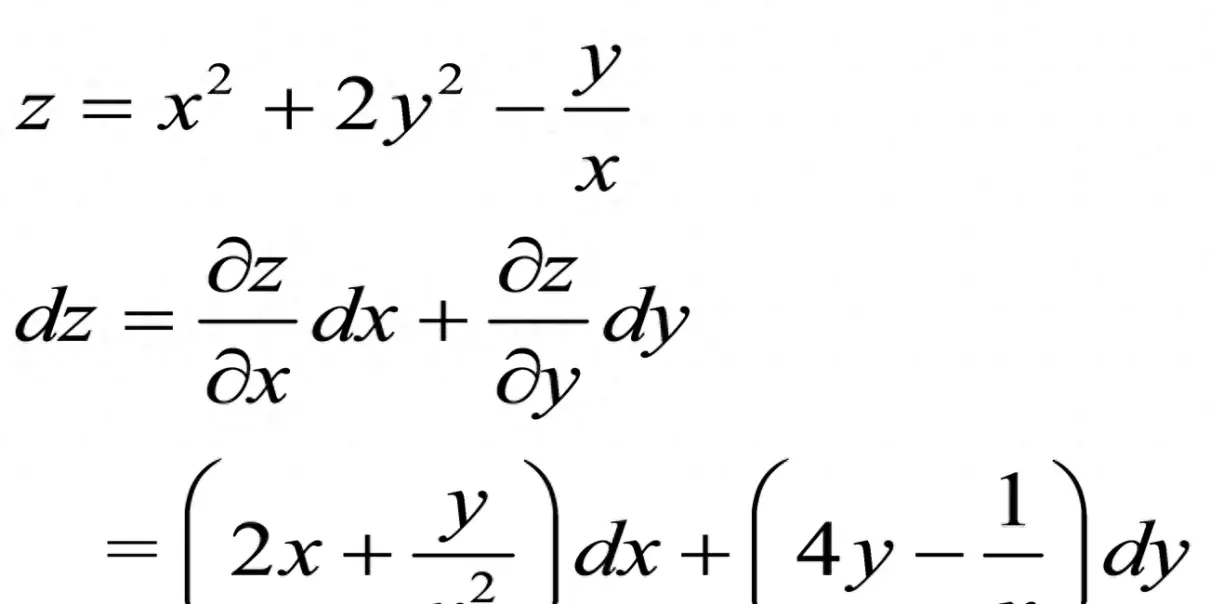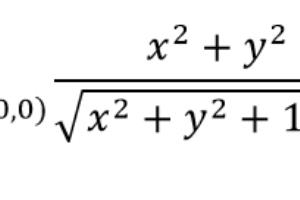以下是一篇关于“二元函数的全微分”的数学类文章的正文部分,共2000字。一、全微分的概念全微分是微积分中的重要概念,主要用于研究函数在某一点附近的变化率。对于二元函数,全微分的概念尤为重要。二元函数的全微分可以通过偏导数来定义和计算。二、二元函数的偏导数偏导数是多元函数在某个特定变量上的导数。对于二元函数,我们可以分别对其两个变量求偏导数。例如,对于函数f(x,y),f'x(x,y)表示f在x方向上的导数,f'y(x,y)表示f在y方向上的导数。通过求偏导数,我们可以得到函数在某一点上的切线斜率,从而了解函数在该点附近的变化趋势。三、全微分的计算公式全微分的计算公式是:df(x,y)=fx(x,y)dx+fy(x,y)dy,其中df(x,y)表示函数f在点(x,y)的全微分,fx(x,y)和fy(x,y)分别表示f对x和y的偏导数,dx和dy分别表示x和y的增量。通过这个公式,我们可以计算出函数在某一点附近的小变化量,从而了解函数在该点附近的变化率。四、全微分的应用全微分的应用非常广泛,例如在近似计算、求极值、判断函数的增减性等方面都有重要应用。特别是在近似计算中,全微分可以帮助我们估计函数的近似值以及其误差范围。例如,当我们需要计算一个复杂函数的近似值时,可以先求出该函数的偏导数,然后利用全微分公式计算出小变化量,从而得到函数的近似值以及其误差范围。五、二元函数的全微分与一元函数的导数的异同虽然一元函数的导数和二元函数的全微分都是用来描述函数的变化率的,但它们之间存在一些重要的差异。首先,一元函数的导数只考虑了单个变量的变化,而二元函数的全微分需要考虑两个变量的共同变化。其次,一元函数的导数描述的是函数在某一点上的切线斜率,而二元函数的全微分描述的是函数在某一点附近的小变化量。这些差异使得二元函数的全微分在实际应用中具有更加丰富的内涵和作用。六、总结通过以上五个方面的阐述,我们可以看出全微分在二元函数中具有举足轻重的地位和作用。从本质上说,全微分是描述函数在某一点附近的变化率的工具。它可以通过偏导数来定义和计算,并可以用来估计函数的近似值以及其误差范围、求极值、判断函数的增减性等方面。在实际应用中,全微分的概念和计算方法具有重要的价值。通过深入学习和理解全微分的概念和性质,我们可以更好地掌握多元函数的本质特征和变化规律,从而更好地解决实际问题。