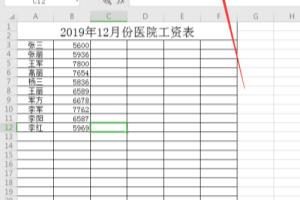
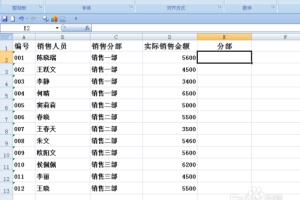
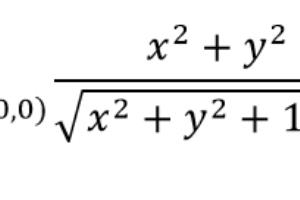x的绝对值在0处不可导因为：
函数 y=│x│是连续函数，但是 y=-x ,y=x , 则在 x=0 处。
其左导数为 lim/△x=/△x= -△x/△x=-1。
其右导数为 lim/△x=/△x= △x/△x=1。
在 x=0 处左右导数并不相等，所以 y=│x│在 x=0 处不可导。
而对于函数 y= x^，导函数为 y'=/3, 在 x=0 处 y'→∞。
即 在 x=0 处左右“导数”皆非有限值，不符合可导的定义。
如果一个函数可导，其必然连续。
如果一个函数连续，则不一定可导。
Y=lXl虽然连续，但导数在0处突变。
函数在一点可导的充分必要条件是连续的函数，在该点的左右极限存在且相等。
函数可导的充要条件是左导数和右导数相等
精彩内容尽在问答鸭，如果您觉得这篇内容不错，别忘了分享给好友哦！
1、双击需要引用数值的单元格，输入“=”，例如我要从另外一个表引用李华等人的语文成绩，则用鼠标双击李华的语文成绩这个单元格，然后输入“=”如图2、点击插入，选择函数，“或选择类别”一项选全部，然后下拉，找到“vlookup”函数，点确定。
1、excel中用函数判断多个条件需要用到or函数。2、or函数的格栗斤式为：=or(logical1,logical2,)。
1、matlab中计算重极限的命令还是用limit，只不过要用多次以实现用累次极限代替重极限。2、下面以计算下面的极限为例来说明matlab中如何计算多元函数的极限。
1、第一步，双击scilab图标，运行scilab软件。2、第二步，创建x变量，并给x赋值，-3.14到3.14，每隔0.02取一个数，并通过y=sin(x)获得与之对应的y的值。
1、首先我们打开一个样表作为例子。2、插入lcm函数，函数的格式是=lcmnumber1，number23、公倍数是只给出的数值共有的倍数，lcm函数求的是其最小公倍数值。
1、启动excel2016电子表格应用软件，如图所示点击屏幕右侧新建空白工作簿。2、按照公司人力资源部数据创建工作簿文档，如图所示。