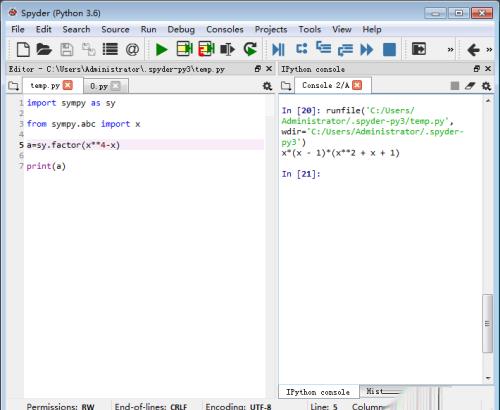
1、四阶域的四个元素，是多项式x^4-x=0的四个解。我们分解这个多项式。分解结果是，三个既约多项式的乘积，其中次数最高的一个因式是二次的。
2、我们要想知道四阶域相对于二阶域的次数，必须在二阶域范围内，分解因式。这也是三个因式，其中一个是二次因式。因此，我们可以说，四阶域相对于二阶域的次数是2。
3、我们要证明，x**2 + x + 1在二阶域里面是既约多项式。
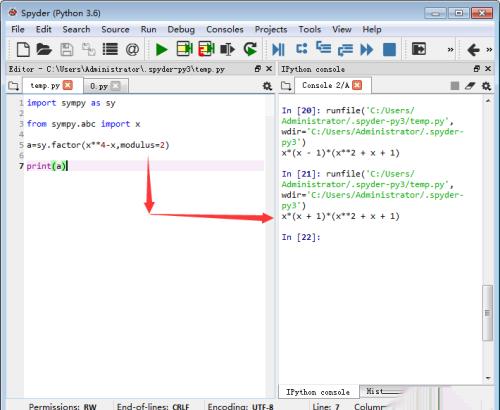
4、因互哨常式x+1=x-1。这毙距说明，多项式x^4-x在整数环和二阶域的分解方法是一样的。
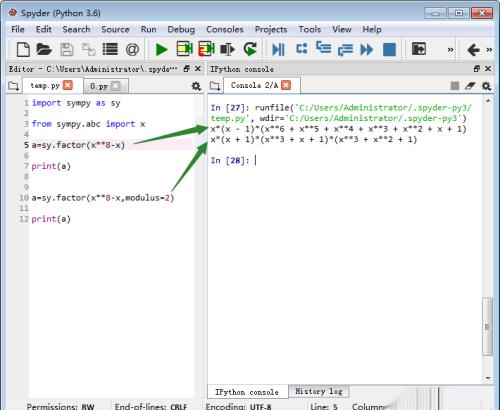
5、作为对比，考虑八阶域，其中的八个元素是多项式x^8-x=0的解捕叮。这个多项式在整数环和二阶域里面的分解因式是完全不同的。
6、这说明，八阶域相对于二阶域是3次扩域。那么请问，怎么计算八阶域的八个元素？
精彩内容尽在问答鸭，如果您觉得这篇内容不错，别忘了分享给好友哦！
1、dnf每天都有5次进入异界的机会，早上六点会重置。2、如果需要增加进入次数，需要使用“异界地下城追加入场券”，可以额外增加一次异界地下城的入场次数，但是不会掉落“勇者装备”。
1、首先点击ppt图标，打开ppt2、在上方选项栏，点击文件选项3、在展开项，点击选项按钮，并进入页面4、在左方功能栏里，找到高级选项5、这时候我们就进入到，修改撤销次数的位置了，输入你想要最多可允许修改的次数6、但要注意的是他最多也仅仅允许修改150次，对于我们来说已经足够了。
二阶域只有两个元素。引进一个新的元素a，使之扩张成一个四阶域。下图就是四阶域的四个元素的一种表现。这四个元素需要在加减乘除之下封闭。