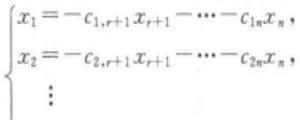首先,我们来了解一下基础解系的定义:基础解系是指方程组的解集的极大线性无关组,即若干个无关的解构成的能够表示任意解的组合。
我们在求基础解系时,先确定自由未知量,我们可以设ax=b的系数矩阵a的秩为r,然后对矩阵a进行初等行变换。
完成初等变换后,将得到的矩阵转化为同解方程组形式。并将自由未知量xr+1,xr+2,,xn分别取值为n-r组数1,0,...,0,[0,1,...,0,...,[0,1,0,...,0。
这时,再将其带入到矩阵的同解方程组中,我们就可以求得矩阵a的基础解系了。我们遇到具体的矩阵时,只需要套用公式即可。
总结
怎么求基础解系:1.确定自由未知量2.对矩阵进行基础行变换3.转化为同解方程组4.代入数值5.求解即可