哈喽,小伙伴们好~
上一篇文章我们讲解了优化算法学习|灰狼优化算法及Python实现,今天我们来学习一下改进混合灰狼优化算法求解作业车间调度问题。
作业车间调度问题通常以最小化最大完工时间为优化目标,因此建立数学模型如下:

01进化种群动态操作
Saremi 等人 在GWO 算法中引入进化种群动态操作 ,就是将种群中差的个体移除,已有研究证明EPD 能够改善整个种群适应度的中值,是一种改进元启发式算法性能的简单有效方法。
在混合灰狼优化算法的每一次迭代中,通过EPD 操作将种群中差的一半个体位置清除,然后在α狼、β狼、γ狼以及局部随机点这四个位置以相等概率重新随机生成它们的新位置。
由于Saremi 等人提出的混合灰狼优化算法是针对连续函数优化问题设计,不能直接用于求解离散的组合优化问题。所以,需要对该操作进行改进,改进后的四个位置更新式如下:

02反向学习初始化种群
对基于种群迭代的群体智能优化算法来说,初始种群的好坏直接影响着算法的全局搜索效率和解的质量,多样性较好的初始种群对提高算法的寻优性能有很大帮助。然而,标准GWO 算法在迭代开始前通过随机初始化产生种群个体,难以确保初始群体的多样性,从而在一定程度上影响了算法的搜索效率。Tizhoosh在2005 年提出了反向学习策略,目前已在GA、DE、ACO 等群体智能优化算法中得到了成功的应用。采用反向学习策略产生初始种群个体的具体操作步骤如下:
在搜索空间中随机初始化N个灰狼个体的位置xi,j 作为初始种群P1。在作业车间调度问题的编码中xi,j ∈中的随机数,D 为每个灰狼个体的维数,即工序总数; N 为种群个数。
(2)生成初始种群P1中每个灰狼个体 xi,j 的反向个体 xi,j' 构成反向种群P2,xi,j'= 1 - xi,j 。
(3)合并种群P1和P2,将2N个灰狼个体按照适应度值进行升序排序,选取适应度值前N 个灰狼个体作为最终的初始种群。
03变异算子
由于基于精英保存策略,在GWO 算法进化后期,群体中所有灰狼个体均向最优个体区域靠近,从而导致种群丧失多样性,如果此时当前最优灰狼个体α 狼为局部最优解,则GWO算法将陷入局部最优,出现早熟收敛现象,这也是很多群体智能优化算法的弊端。为了降低GWO 算法出现早熟现象和陷入局部最优值的概率,本文对群体中当前最优灰狼个体α 狼进行多样性变异操作,其原理是: 对最优个体α 狼中的每一维元素以1 /D 的概率进行变异。变异操作公式为:

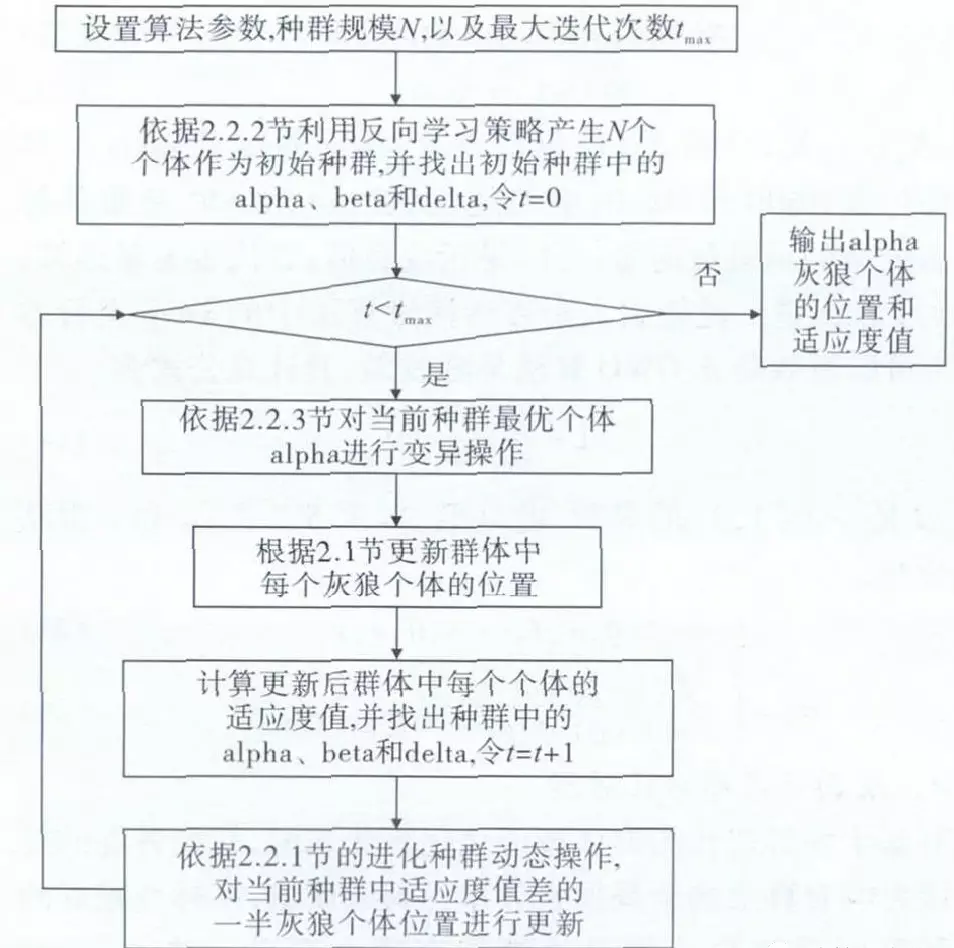
通过对标准GWO 算法进行进化种群动态、反向学习初始化种群,以及最优个体变异三方面的改进操作,改进后的混合灰狼优化算法拥有更佳的寻优性能,同时跳出局部最优解的能力更强。运用所提出的IGWO 算法求解作业车间调度问题的算法流程如图1 所示。
Saremi S , Mirjalili S Z , Mirjalili S M . Evolutionary population dynamics and grey wolf optimizer. Neural Computing & Applications, 2015, 26:1257-1263.
Yang X . Nature-Inspired Metaheuristic Algorithms: Second Edition. 2010.
Tizhoosh, H. R . Opposition-Based Learning: A New Scheme for Machine Intelligence// International Conference on International Conference on Computational Intelligence for Modelling, Control & Automation. IEEE, 2005:695-701.
[4]姚远远,叶春明.求解作业车间调度问题的改进混合灰狼优化算法[J].计算机应用研究,2018,35(05):1310-1314.